为什么三全音（增四减五）让人觉得压抑和诡异？

（本文来源：知乎；作者：萌铁蛋 MnFeN）

依然将这句作为第一句：音程的听觉感受与其数理本质有着密切关系。

学界通常认为一个音程中两个音的听觉感受是否协和取决于其数理本质：两个音的频率是否接近整数比（其本质是两个音的声波叠加后是否具有短周期）。（也就是说，是取决于两个音之间的共振，而不是声音与人体的共振。）

举几个栗子：

除了纯一度以外最协和的纯八度（C−c）的频率比为 1 : 2；纯五度（C−G）的频率比接近 2 : 3；纯四度（C−F）接近 3 : 4；大三度（C−E）接近 4 : 5；小三度（C−E♭）接近 5 : 6；……

随着频率对应的整数比的复杂化，以上音程的听觉感受的协和性也逐渐降低。

比如乐理中会提到，纯八度的感觉是“纯净”；纯五度、大三度是“开阔、愉悦”；小三度的感觉是“忧伤”（注：不只是听觉的生理原因，也有一定的文化背景）。

而对于不协和音程，如三全音（C−G♭）、小二度（C−D♭），其描述通常是题主所谓的压抑、紧张、诡异。看一下它们的频率比就知道了：三全音的频率比为 2^1/2，接近的整数比为 12 : 17；小二度的频率比为 2^1/12 ，接近的整数比为 18 : 19 ——相比以上协和音程的整数比，可见其非常不协和。

说完音程再来说属七和弦。其实人的感知体系是很复杂的，单纯用简单整数比这一套解释未免有些先验的感觉，在此只是结合学界通常的观念以及自己的听觉感受和理解进行介绍。

属七和弦 5 7 2 4 有强烈的被解决的倾向，而这种倾向从何而来？科学上有种研究方法叫控制变量法，我们可以通过把影响不大的音剔除进行分析。减三和弦 7 2 4 依然有这种不协和感，而再剔除掉 2 的三全音 7 4 仍是如此。即使单纯听到这两个音的时候很多人都会有接上 1 3 的感觉，由此可见三全音的确是属七和弦不稳定的重要因素，这也与学界目前普遍的观点一致（其实还有一部分 5 4 这一组小七度的影响）。

那么是否能利用三全音的这一性质组合出更不协和的和弦呢？可以了解一下减减七和弦（1, ♭3, ♭5, ♭♭7=6）。减减七和弦可以看做小三度的多次叠置，而且每两个小三度的叠置便产生了一个减五度，所以这一个和弦便包含了两个减五度音程。注意第四个音 6 和下一个八度根音 1 也是小三度关系，所以这个和弦可以一直叠置上去，便会一串包含更多的减五度音程的音列（其实模仿「十二平均律」的说法，可以把这个强行叫成「四平均律」23333）。

以下音频为贝多芬的 Appassionata 中的一段，第三至第十个音便是两个八度内减七和弦的分解：

最后补充一点：为什么简单整数比的声音会被认为和谐呢？

初中物理课学习声音的时候应该提过，乐音是有规律的振动，而噪音是无规律的振动。这个规律，可以看做声波的波形图的周期。

下面是纯音、纯四度、大三和弦、三全音的波形图——

首先是纯音（不考虑声音随着时间的衰减），其波形图就是简单的振幅恒定的正弦波：

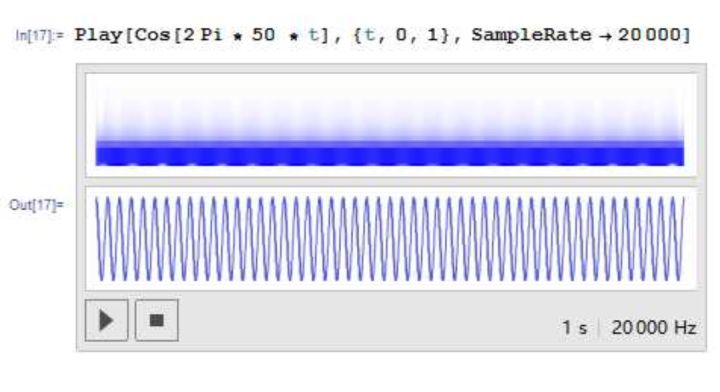
而对于纯四度、大三和弦，波形图仍然可以看出一个较小的周期，而每两个周期波形和振幅完全相同，也就是说它们还算是「有规律的振动」的乐音：

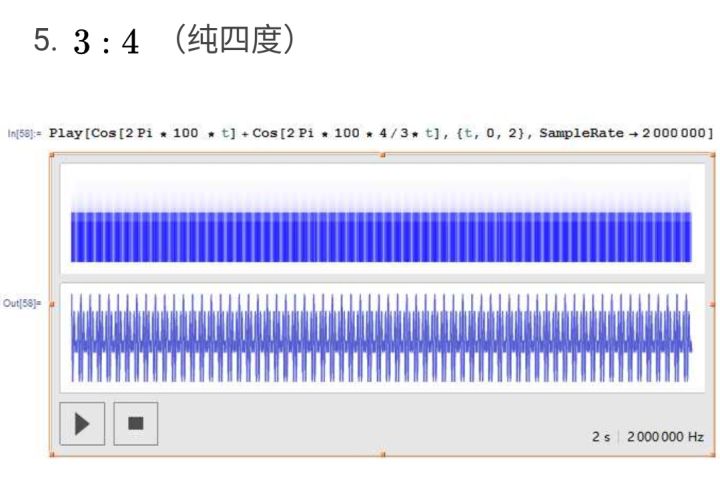
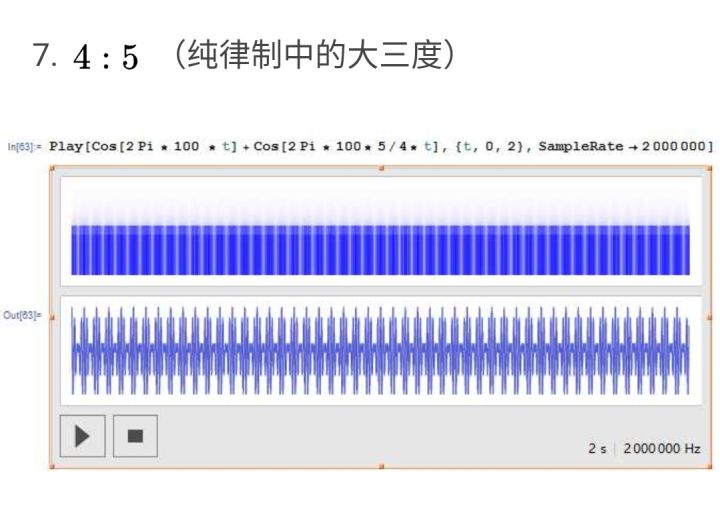
而对于下面这张无理数比例的三全音波形，则并不能看出明显的周期，所以协和感较差。

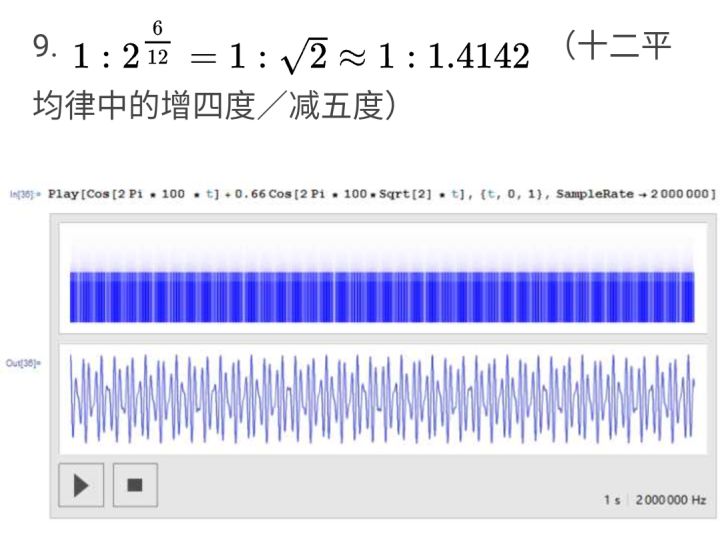
所以总结一下：简单整数比例频率的声音的叠加产生的仍然是具有明显周期性的乐音，这是这类音程或和弦听觉感受比较和谐的原因之一。

P. S.  本文基于十二平均律，即相邻两个半音的频率比为定值 2^1/12 ，很多乐器（如钢琴、吉他）使用的均是此律制。该律制在转调的方面有着无可比拟的优点，但使得一些原本恰为整数比的协和音频率比变为近似的无理数 2^n/12，所以文中多处提及「接近」。